Python descriptor details

伪随机数： 线性同余法的应用

1. 背景

在传统游戏AI业务中，经常会用到随机数来避免机械化的行为。比如，以行为树（BehaviourDesigner）实现的AI需要使用到随机数来产生随机行为，从而避免重复动作，增加AI行为的多样性。同时，又因为帧同步的要求，需要保证在不同设备或者回放（重新跑帧逻辑）时产生的结果是一致的。所以，我们通常会选择伪随机数发生器来完成随机要求。

另外，在我们项目中，对于产生的伪随机数还有一些额外要求：

1. 在同一帧内，不同AI个体产生的随机数结果要相互独立（i.e. 也就是A个体的随机结果和B个体的随机结果间不能存在某种关系）。这样可以避免多个AI走同一套AI逻辑时，如果所处环境很类似，会产生一样的行为的情况。视觉看上去这是多个AI出现了行为一致，很容易被看出来是AI。

2. 在同一帧内，同一AI个体多次调用随机数接口产生的随机数结果应该保持不变。这是因为我们的AI模块中会有难度设置，不同难度下需要通过一个随机概率来调节AI做出某种行为的概率。例如，低难度下AI做出进攻行为的条件应该是A的攻击力(100)*调节概率(0.8) > threshold。此时的调节概率是随机出来的值，但是该节点可能会在一帧内执行多次，或者一帧内会有多个节点会使用到这个调节概率。所以，为了保持一帧内的结果一致，需要保证一帧内同一AI个体多次调用随机数接口时产生的结果一致。

3. 在不同帧内，同一AI个体产生的结果应该独立。这是最基本最常见的随机数的使用要求。一般来说，只要合理选择线性同余发生器的参数，则可以在其周期范围内认为其产生的结果是均匀的。

2. 线性同余法

线性同余法应该是使用最多的伪随机数方法，如果能够选择合适的参数，对于一般的随机要求是足够的。其核心原理则是通过不断取模在一个模数范围内取得每次的值。只要模数足够大，且是满周期，则可以认为在这个模数范围内取得任一值的概率是相等的。其核心公式为：

$$X_n = (a*X_n-1 + c) % m$$.

这里我们从gcc的实现上来看：

// 此套参数为 a = 1103515245, c = 12345, m = 32768
static unsigned long next = 1;

/* RAND_MAX assumed to be 32767 */
unsigned myrand(void) {
    next = next * 1103515245 + 12345; // 修改种子
    return((unsigned)(next/65536) % 32768); // 返回伪随机结果
}

void mysrand(unsigned int seed) {
    next = seed;
}

这里有几个值得注意的地方：

• 在myrand()函数中，next表示的就是种子。这里每次调用该函数，会先修改此次随机行为的种子为next * a + c。但是按照线性同余法原本的定义，下一次随机的种子应该为(next * a + ) % m，但是在gcc的实现中利用了整数的溢出规则，让其超过整形限制时自动实现取模操作。这种方法在滚哈希的时候常用，理论上会比手动取摸更快（寄存器自然操作）。

• 在计算随机结果的时候，先对种子进行了next/65536的操作，这一步为了抛弃低位数字。因为高位数字比低位数字具有更长的周期，所以这样会产生更均匀的随机数。

  As shown above, LCGs do not always use all of the bits in the values they produce. For example, the Java) implementation operates with 48-bit values at each iteration but returns only their 32 most significant bits. This is because the higher-order bits have longer periods than the lower-order bits (see below). LCGs that use this truncation technique produce statistically better values than those that do not. This is especially noticeable in scripts that use the mod operation to reduce range; modifying the random number mod 2 will lead to alternating 0 and 1 without truncation.

  ​ —- wiki

简单总结，每次调用myrand()函数，都会经历一次修改种子，计算随机结果的操作。只要这样不断更新种子，才能保证取到的伪随机数是真正在周期范围内（m内）只均匀出现过一次的数。很显然，传统的LCGs是不能满足我们对于随机数的要求1和要求2，（要求3天然满足）。因此，我们需要对LCGs进行修改。

3. 在每帧开始固定一个随机数种子

我们最开始的想法，是在每帧开始前先固定一个随机数种子，然后对于不同的角色，根据其id对种子做偏移以取得不同的结果。代码如下：

static unsigned long seed = 1;

// 一帧内不同英雄都可能多次调用此函数
unsigned myrand(){
    if(curFrame != GetFrame()){
        seed = seed * 1103515245 + 12345;
        curFrame = GetFrame();
    }
    rand(obj_id);
}

unsigned rand(void, obj_id) {
    // 往下在取一次种子，同时使用playerId区别不同角色随机的结果
    unsigned long nextSeed = (seed + obj_id) * 1103515245 + 12345; 
    return((unsigned)(nextSeed/65536) % 32768); // 返回伪随机结果
}

从代码中可以看到，此时会在每一帧开始时先固定一个种子，然后对于不同的obj_id，在该种子的基础上往后取一次种子，同时以该id作为偏移量。咋一看这样确实满足了背景上的三个条件，但是其实存在问题。在LCGs中，如果种子固定，那么在该种子上作偏移，始终是存在一定的线性关系。举个例子，如果此时myrand(playerId = 1)的结果为28，那么myrand(playerId = 2)的结果大概率为大于28的随机数（说大概率是因为可能存在溢出的情况）。具体可以看下图：

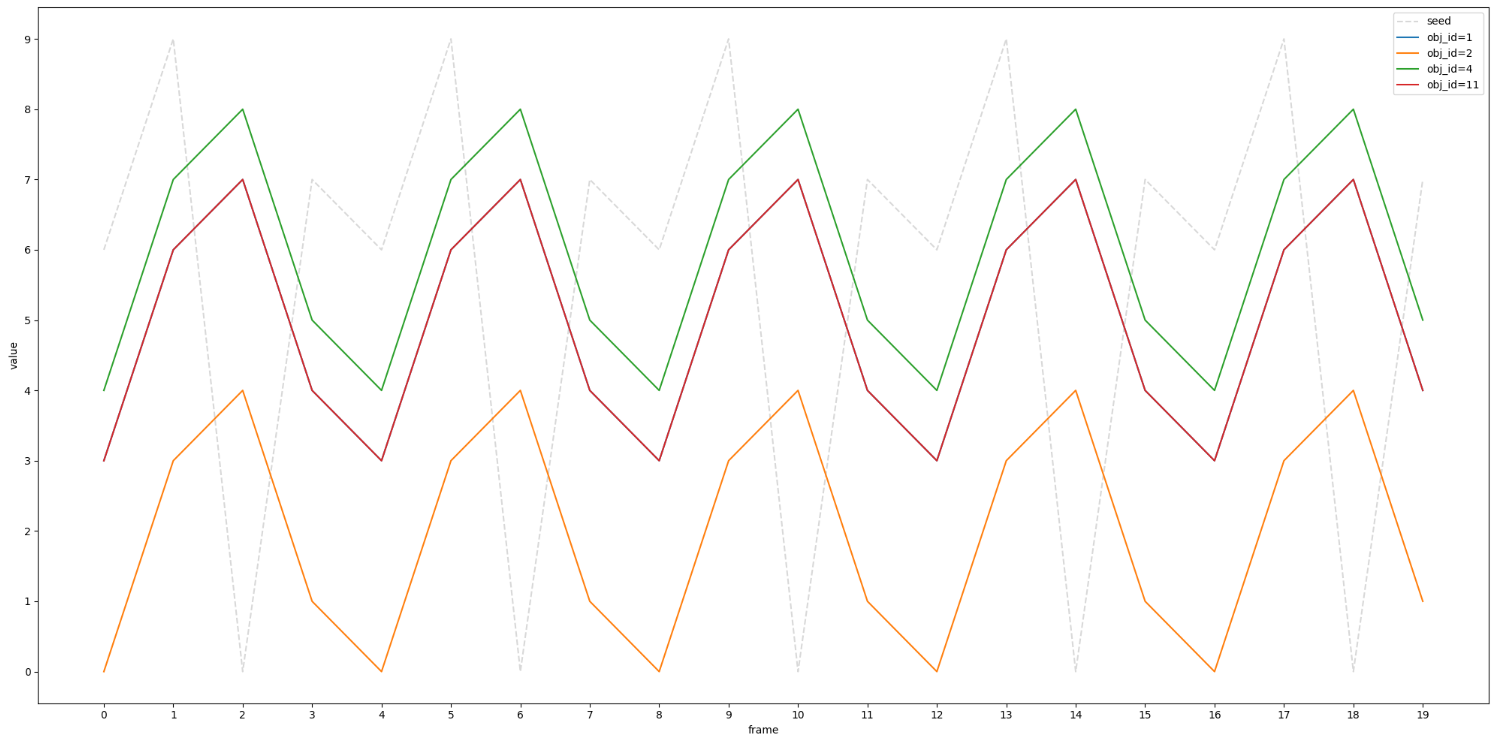
该图中所使用的的参数为：a = 7, c = 7, m = 10, s0 = 7,从图中可以看出，obj_id = 4和obj_id = 11明显有着同样的“距离”。也就是说，在同一帧中，不同的玩家，随机到的结果却是始终出现了类似的结果。如果体现在AI上，就是不同的AI个体，但是在随机做一些动作时，总是会随到同样的动作。或者随机往某个方向移动时，总是会随机到类似的方向。这就导致AI的拟人化很差，人类玩家一样就能看出来AI。

这个结果其实也很容易推论出来，根据LCGs的公式：(a*(s+o)+c)%m -> ((a*s+c)%m + (a*o)%m)%m，当s固定时，左侧加数其实是一个常数，也就是只有(a*o)%m在变化，当a*o小于m时这其实就是条直线，大于m后就溢出重来。 我们可以画一个更极端的图来验证：

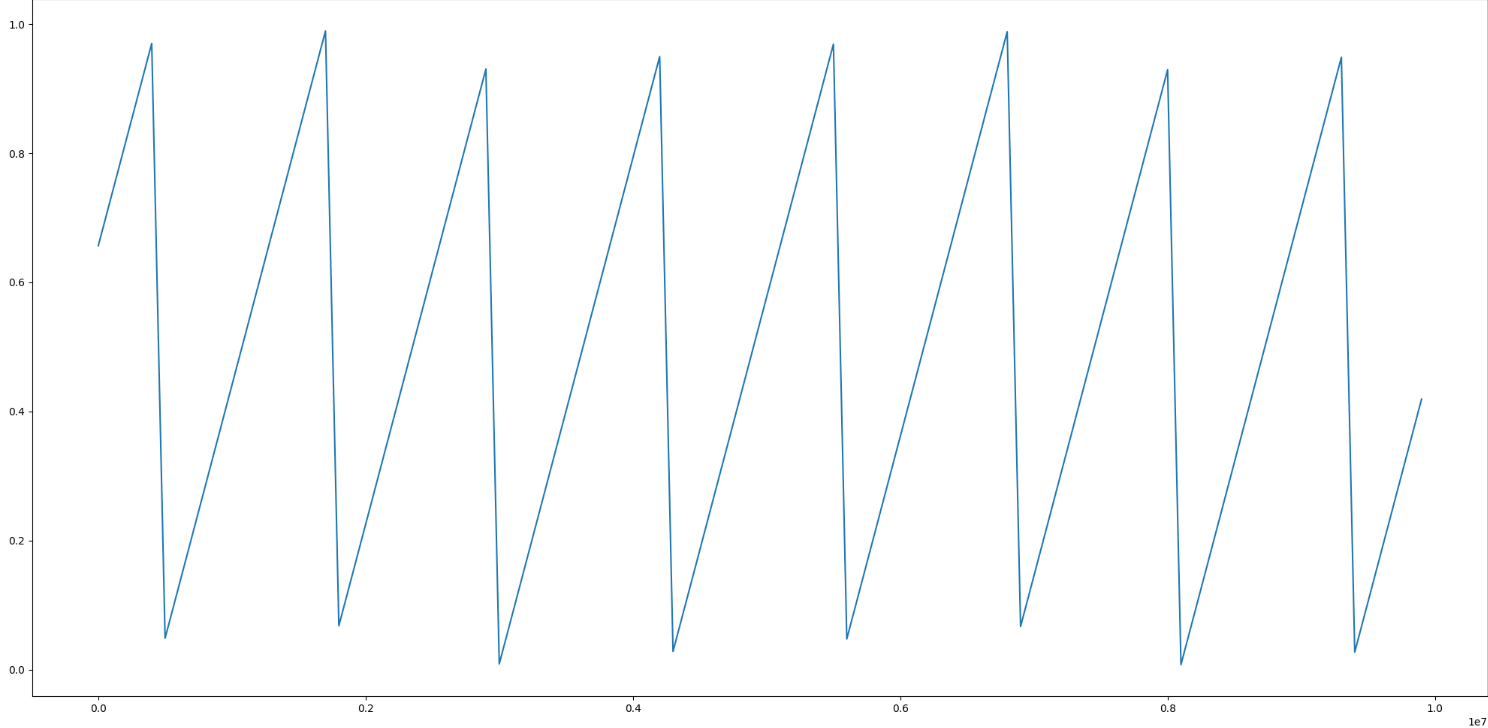
该图为固定一个种子后，obj_id（x轴）从0不断增大，随机值（y轴）的变化。可以看到，随着obj_id的增大，其值总是在不断增加，然后溢出重来。这就导致对种子进行偏移来区分不同对象以取得不同随机数的方法是不对的，因为他们取到的值并不是均匀的， 而是具有一定的差值。此时并不满足我们背景里的要求1，即不同角色取到的随机数并不是独立的，而是存在一定差值。

4. 对obj_id先做一次rand()

上述方法并不满足我们的3个要求，因为当obj_id一定时，以其作为偏移量，得到的随机结果也总是有一定的偏移量。所以，我们可以先对obj_id取一次随机，然后将得到的结果作为偏移量。

static unsigned long seed = 1;

// 一帧内不同英雄都可能多次调用此函数
unsigned myrand(){
    if(curFrame != GetFrame()){
        seed = seed * 1103515245 + 12345;
        curFrame = GetFrame();
    }
    int result = rand(rand(obj_id));
}

unsigned rand(int offset) {
    unsigned long nextSeed = (seed + offset) * 1103515245 + 12345; 
    return((unsigned)(nextSeed/65536) % 32768); // 返回伪随机结果
}

这样其实也是和上面的方法存在一样的问题。因为第一次rand的时候，得到的offset其实也是存在一定的差值的，所以第二次rand这个差值并不会消失。

5. 每帧缓存不同obj_id的结果

根据上面的分析，可以知道其实只有在LCGs的迭代公式上才能获得均匀的伪随机数，如果固定种子做偏移是不行的。所以，为了满足上面三个条件，可以有一种方法：将obj_id看作是执行rand的次数，而不是在种子上做偏移。比如rand(5)则表示调用5次rand函数，也就是在迭代公式上走了5次，返回的当然还是随机的结果。这样的做法，对于每帧内不同的obj_id，返回的肯定是独立的结果。并且，每帧内由于基seed并不会改变，所以同一个obj_id多次调用，返回的也是同样的结果。即满足上述的所有三个条件。

但是这样会有大量的浪费（如果obj_id很大）。所以，有一个折中的方法为：如果obj_id的数量不是很多的话，例如固定100个，那么可以用一个字典来缓存每帧内的随机结果：

static unsigned long seed = 1;
dictionary <int, int>* randomResults;

// 一帧内不同英雄都可能多次调用此函数
unsigned myrand(){
    if(curFrame != GetFrame()){
        randomResults->clear();
        curFrame = GetFrame();
    }
    unsigned result = rand(rand(obj_id));
}

unsigned rand(int obj_id) {
    unsigned result = 0;
    if (!randomReuslts->tryGetValue(obj_id, &result)){
        seed = (seed + offset) * 1103515245 + 12345; 
        unsigned result = (unsigned)(seed/65536) % 32768);
        randomResults->Insert(obj_id, result);
    }
    return result
}

从代码里可以看出，同一帧内并不是固定一个seed，而是每次调用到rand函数都会更新seed，但是在刚进入到新一帧时，会先清空缓存的字典。然后每一个不同的obj_id，都会作为key存入字典中。也就是说，后续如果有相同的obj_id再次调用rand函数，则不会真正的再去取一次随机数，而是从缓存里得到该帧内第一次随机得到的结果。也就是满足了是三个条件中的条件2。同时，因为此时并没有在固定种子上做偏移，而是和LCGs的常规用法一样，每次调用都会更新种子，所以返回的也是均匀的伪随机数，所以满足了条件1。条件3则是天然满足。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 gzrjzcx@qq.com